[인사-23010] IPA분석과 직원 몰입도 및 만족도 조사_R언어
Ⅰ. "그래서? 가장 먼저 해야할 것이 뭐죠?"
우리 부서 위로 새로운 리더(부사장)가 발령나자, 우리 팀은 분주하게 그간의 업무 경과와 향후 업무계획 등을 준비하여 보고를 드렸다. 삼성 임원 출신이였던 그 리더는 인상을 찌뿌리며 우리가 작성한 보고서를 빠르게 읽어내려 갔고, 그의 손에 쥐어진 빨간펜은 쉴새없이 움직였다.
연세는 있지만 눈동자만큼은 강렬했던 당신이 드디어 입을 열었다.
그래서? 가장 먼저 해야할 것이 뭐죠..?
여기서 가장 본질적인 것들을 추려내서 중요도 체킹하고 우선순위를 매겨주세요.
우리들이 보유한 자원과 역량은 한정되어 있는 반면에 처리하여야 하는 문제는 산적해 있는 경우가 왕왕있다. 전장에서 각개격파 전술를 활용하는 것처럼 대부분의 사람들은 문제를 맞닥드리면 해결이 필요한 과제들의 중요도와 난이도, 그리고 긴급성 등을 기준으로 우선순위를 설정하여 해결한다.

인사노무 영역도 마찬가지라고 생각한다. 조직이 해당 영역에 투하할 수 있는 자본은 한정되어 있으므로 인사노무 담당자는 직원들의 소속감 강화, 상사 및 직무에 대한 만족도, 근무환경 및 복리후생, 조직 내 커뮤니케이션의 원활화, 직원들의 경력 및 진로개발 기회 정도 등 다양한 이슈 혹은 개발이 필요한 다양한 역량들 사이에서 무엇을 먼저 집중적으로 다뤄야 하는지 결정할 필요가 있다.
인사관리상 문제는 마케팅(혹은 영업)의 문제와 유사한 특징을 지니고 있는데, 인사관리는 기업 내부 고객인 직원을 대상으로 하는 서비스이기 때문이다. 회사와 종업원의 관계는 과거의 가족 중심적인 성격에서 벗어나 철저히 계약에 의한 관계로 변해가면서 기업과 종업원 모두 서로가 가진 채무의 가치를 저울질 하며 회사는 해고를, 종업원은 퇴사를 고려한다.
따라서 회사는 핵심인재의 이탈 등을 방지하기 위해서라도 회사와 종업원 간의 교환관계가 공정하도록 신경써야 한다. 그러나 교환관계는 상대적인 판단이 개입할 수 밖에 없다. 가령, 회사는 이 정도면 해줄 만큼 해줬다고 생각했지만 어떤 종업원은 그렇지 않다고 느끼는 반면에 다른 종업원은 상당히 만족할 수도 있다는 것이다. 그렇기 때문에 회사는 종업원이 인식하고 있는 교환가치의 무게를 객관적이고 정량적으로 분석할 수 있어야 하고, 이를 위하여 사회과학 연구가 필수적이다.
결국, 회사는 조사와 연구를 통해서 직원들이 인사관리 서비스 항목 중 ①무엇을 더 중요하게 생각하고 있으며, ②그것이 주는 만족감(높은 교환가치로의 인식)이 어떠한지를 분석해 가장 효율적으로 HR 자원이 배분될 수 있도록 우선순위를 결정을 하여야 한다.
Ⅱ. IPA(Importance-Performance Analysis) 개념

앞서 인사관리에 존재하는 문제는 마케팅 분야가 직면하는 문제와 유사하다고 말했다. 마케팅에서 사용되는 여러가지 분석 방법과 개념은 실제 인사관리 영역에서도 적용될 수 있는 것들이 꽤 있다. IPA(Importance-Performance Analysis)도 그러한 것들 중에 하나다.
IPA는 Martilla & James가 개발하여, 1977년 Journal of marketing에 해당 내용에 관한 논문을 발표하면서 세상에 등장하였다. 특정한 제품을 구성하는 여러 가지 요소들 가운데 어떠한 것이 소비자들에게 주로 어필될 수 있는지를 검토함으로써 다음 제품 출시에는 이를 개선하거나 보완할 수 있도록 시사점을 얻기 위해 실시하는 분석 기법이다.
가령, A라는 게임을 소비자들에게 제공하고 나서 ①스토리, ②그래픽, ③케릭터 모델링, ④성우들의 더빙, ⑤게임 밸런싱 등에 대하여 IPA 분석을 통해 향후 게임 출시 시 그래픽을 강화해야 할지 혹은 스토리를 보완하여야 할지 시사점을 얻는다.
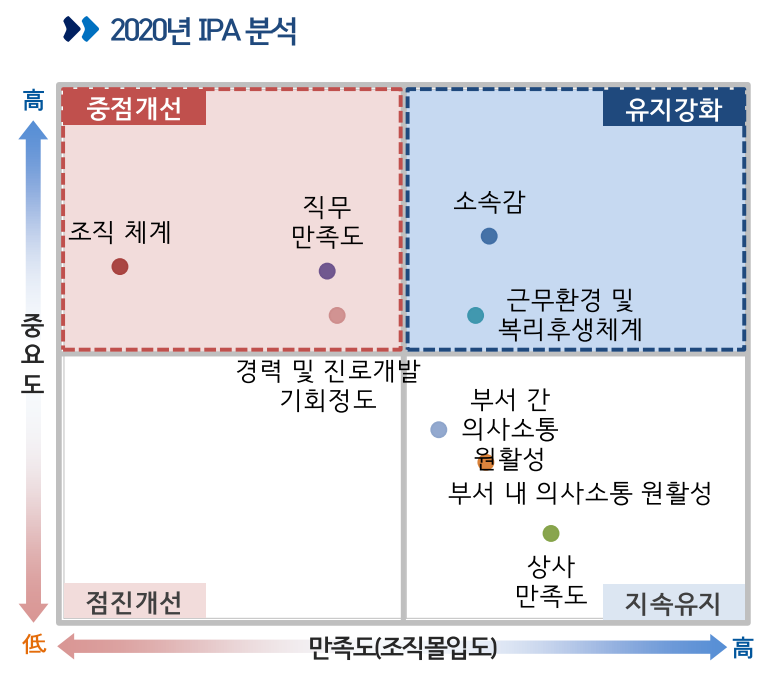
인사관리에서도 IPA는 유사하게 사용된다. IPA는 중요도와 만족도라는 두 가지 축을 사용하여 2차원 점 도표를 작성한다. Y축으로 작성되는 중요도는 직원들이 중요하다고 느끼는 정도를 수치화한 것이고, X축은 직원들이 현재 해당 항목에서 느끼고 있는 직접적인 만족도를 말한다.
위 예시 그림의 기업에게는 ⓐ직무 만족도, ⓑ경력개발, ⓒ조직체계라는 카테고리의 서비스를 다른 인사관리 서비스에 비하여 우선적으로 투자 및 개발하는 것이 직원 사기 진작과 조직 몰입 강화에 효과적일 것이라는 시사점이 도출될 수 있다.
그럼 이제 본론으로 들어가서 중요도와 만족도는 어떻게 구하는 것인지 살펴보도록 하겠다.
Ⅲ. R을 이용한 IPA 분석 방법
1. 가상 데이터 제작
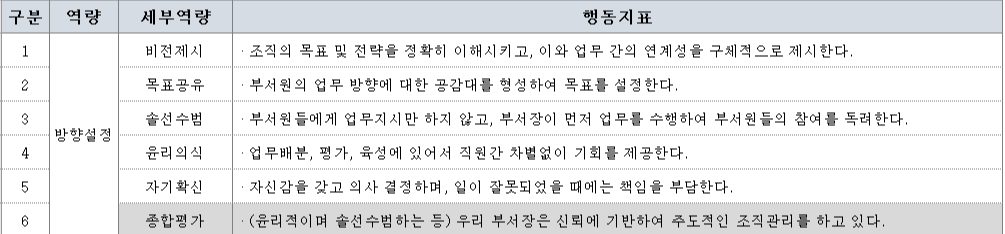
IPA를 분석하기 위해서는 어떠한 평가항목(위 그림 "방향설정")에 대한 전반적인 평가(위 그림 "종합평가")와 평가항목에 대한 각각의 세부 평가들(위 그림 비전제시, 목표공유 등)로 구성된다. 이렇게 구성하는 이유는 이후 중요도를 산출하는 과정에서 다시 한번 더 설명하도록 하겠다.
random_data = data.frame(
Total_Satisfaction = sample(1:5, 30, replace = TRUE),
Partial_Satisfaction_A = sample(1:4, 30, replace = TRUE),
Partial_Satisfaction_B = sample(1:3, 30, replace = TRUE),
Partial_Satisfaction_C = sample(1:2, 30, replace = TRUE),
Partial_Satisfaction_D = sample(3:5, 30, replace = TRUE)
)랜덤 데이터를 발생시키는 코드를 작성하였다. 대충 봐도 이제 감이 올 것으로 생각이 드는데, 예상했던 것처럼 Total_Satisfaction이 위 그림에서의 "종합평가"이고, 나머지 Partial_Satisfaction은 "세부역량"들을 표현한 것이다. 복잡해질 필요는 없으므로 30명이 응답했다고 가정하여 랜덤 데이터를 데이터 프레임 형태로 만들었다.
2. 중요도와 만족도 계산하기
# Load the ppcor package
library(ppcor)
library(tidyverse)
# Calculate the partial correlation coefficients
pcor_result = pcor(random_data)
# To calculate Importance
Importance = pcor_result$estimate[2:5]/sum(abs(pcor_result$estimate[2:5]))
# Average Partial variable
partial_means = colMeans(random_data[, grepl("^Partial_Satisfaction", colnames(random_data))])우선, 중요도와 만족도를 구하기 위해서 탐색적 요인분석 등을 통해 설문항목의 신뢰성 및 타당성을 검증하는 것이 순서이긴 하나 여기서는 과감히 해당 내용은 생략하고 진행하도록 하겠다.
중요도(Importance)는 설문조사를 통해 직접 값을 구할 수도 있으나, 본문은 전반적인 만족도(Total_Satisfaction)와 개별 만족도(Partial_Satisfaction) 간의 편상관계수(Partial Correlation)를 통해 구하였다. 이와 관련해서 일반적인 상관관계나 회귀분석을 통해 계수값을 이용할 수도 있으나, 최근에 수행된 연구결과에서 편상관계수 값을 사용하는 것이 좀 더 바람직하다는 보고가 몇 차례 있어 필자의 경우에는 편상관계수 값을 활용하였다.
생각컨대 일반 상관관계 값은 교란변수에 의해 값이 왜곡되어 온전한 결과값을 도출하는 것이 어려울 수 있다고 생각한다. 예를 들면 위 그림 예시에서 세부역량 중 "비전제시" 항목과 "목표공유" 항목은 약간 중첩된 내용일 수 있어, 종합평가 항목에 비전제시 항목과 목표공유 항목이 미치는 영향력이 다소 희석되거나 튈 수 있다. 따라서 종합평가 항목과 비전제시 항목 둘 간의 상관관계를 목표공유 항목이 영향을 미치지 못하도록 통제시킨 뒤에 구하는 편상관계수 값을 이용하는 것이 중요도의 민감도를 관측하는데 더 효과적일 것으로 보인다.
편상관계수는 ppcor 패키지를 통해 구할 수 있다. 각각의 상관계수 값은 아래와 같은 구조로 나타난다.
Total_Satisfaction <-> Partial_Satisfaction_A : -0.2623886
Total_Satisfaction <-> Partial_Satisfaction_B : 0.1750279
Total_Satisfaction <-> Partial_Satisfaction_C : 0.1198384
Total_Satisfaction <-> Partial_Satisfaction_D : 0.2809910
중요도는 편상관계수 값을 모두 더한 값을 각각의 상관계수 값과 나누어 계산한다. 다만, 이때 마이너스 계수값이 있을 수 있으므로 abs() 기능을 이용해 절대값으로 계산을 진행한다. 그렇게 계산한 것이 pcor_result$estimate[2:5]/sum(abs(pcor_result$estimate[2:5]))라는 코드로 표현될 수 있다. 이후 각 항목별 만족도(Satisfaction)는 평균값으로 계산하여야 하여 리스트 형태로 저장해둔다.
※ 통상적으로 마이너스 계수값이 등장하는 경우는 드문데, 있다면 설문조사 항목 등을 면밀히 재검토해볼 필요가 있다. 그럼에도 불구하고 이상이 없다면 그대로 진행해도 무방하다.
3. IPA 도표 그리기
## Create dot plot
# Data preparing
partial_means_df = data.frame(
Satisfaction = names(partial_means),
Mean = partial_means,
Importance = Importance
)
# Add average lines
avg_imp = mean(partial_means_df$Importance)
avg_mean = mean(partial_means_df$Mean)
# make the plot
p = ggplot(partial_means_df, aes(x = Mean, y = Importance, color = Satisfaction)) +
geom_point(size = 4) +
labs(x = "만족도", y = "중요도") +
theme_classic() +
theme(legend.position = "none") +
geom_text(aes(label = Satisfaction), vjust = -1) +
geom_vline(xintercept = avg_mean, linetype = "dashed", color = "black", size = 1) +
geom_hline(yintercept = avg_imp, linetype = "dashed", color = "black", size = 1)
# Display the plot
p도표를 그리기 위한 재료로 Partial_means_df라는 데이터 프레임을 만들어주고, 이후 도표에 평균값의 점선을 표시할 수 있도록 중요도, 만족도 각각의 평균값을 구해준다.
이후 ggplot을 이용해 도표를 생성하면 아래와 같은 도표가 완성된다.

이 도표를 해석하면 Partial_Satisfaction_C와 Partial_Satisfaction_B를 우선적으로 관리 또는 투자하여야 한다고 볼 수 있다. R은 정말 Python에 비해 너무 쉽고 빠르다는 것을 실감한다.
[참고 문헌]
보누스 출판사, 나폴레옹은 단 한 가지 전술로 유럽을 평정했다, 시리즈 전술의 본질, 2020. 11. 13.
[SPSS 리서치] 13. IPA 분석(만족도-중요도 분석)
- URL : https://sooupforlee.tistory.com/entry/SPSS-%EB%A6%AC%EC%84%9C%EC%B9%98-13-IPA-%EB%B6%84%EC%84%9D-%EB%A7%8C%EC%A1%B1%EB%8F%84-%EC%A4%91%EC%9A%94%EB%8F%84-%EB%B6%84%EC%84%9D